https://ieeexplore.ieee.org/document/9134370
長いので分割することに。
この記事はIntroduction, Related Work, Overview, Data Based ApproachのInstance Weighting Strategy。
Introduction
ある分野の知見をほかの分野に転用することが転移学習のやりたいこと。例えば、将棋からチェス、バイオリンからピアノなどである。
だが、なんでも転移すればいいというものではない。スペイン語からフランス語へは、知っているが故に間違えることがあり、Trasnfer LearningではNegative Transferという。
Transfer Learningは2つに分けられる。
- Homogeneous これは同じ特徴空間の上での転移学習を行う。同じ特徴空間の上なので、Domainの違いはが違うことだけ。
- Heterogeneous 違う特徴空間の上での転移学習を行う。違う特徴空間の上なので、まさに知識を転移するということになる。
Related Works
比較的に近い各分野について、転移学習との違いを説明する。
Semi-supervised Learning
LabeledとUnlabeled両方で学習を行うが、同じDomainから選んでいることに注意。とはいえ、多くの技法(クラスター仮説など)を借りてくることもできる。
Multi-view Learning
複数の視点から学習する=複数の特徴でそれぞれ学習するというもの。部分空間学習、マルチカーネル学習、co-trainingなどがある。
Multi-task Learning
複数のタスクの中で共同する知識があるだろうということで、それらを共有しつつ同時に学習を進めていく。📄2020-NIPS-Gradient Surgery for Multi-Task Learning こことかがいい例。
違いとしては、どちらも知識の転移をやりたく、それを実現するためにパラメタの共有、特徴量変換などの手法を共有することがある。しかし、
- 同時に学習しながら情報を共有し合うMulti-task Learning
- すでに学習が済んだか、知識を持っている状態で新たに別のタスクを学習するTransfer Learningという構図。
Overview
Domainの定義
Domainとは、特徴空間と、そのうえのサンプルの周辺分布によって構成される。
Taskの定義
Taskとは、ラベル空間と、識別器について以下のように構成される。
Transfer Learningの定義
以下の図が一番わかりやすい。
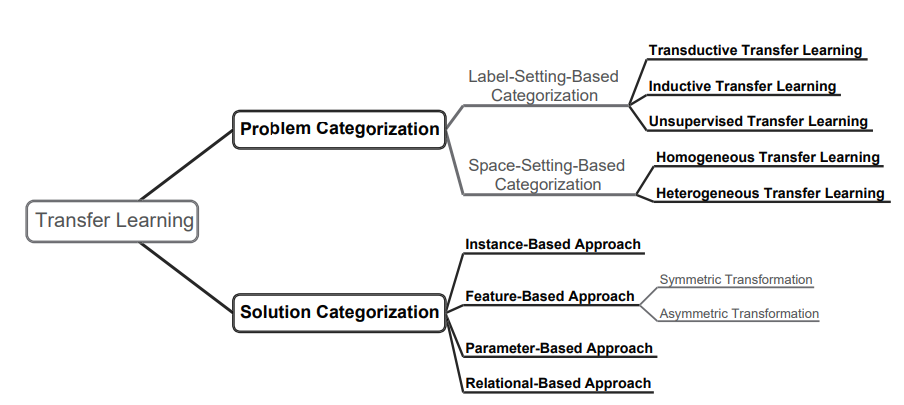
ソースドメインという学習するデータの存在するのは、個のDomainから構成されると考える。つまり、このように複数のソースドメインから学習データが集められる。
次に、ターゲットドメインという予測したいデータが存在するDomainは同様に、個のドメインで構成される。つまり、である。
転移学習の目標は、をうまく、ソースドメインから学習をすることである。
ならば、Single Source Transfer Learningであり、そうでないならMulti Sourceになる。については特に名称はないが、もちろん多いほど難しい問題になる。
一番簡単なのは、である。
Domain Adaptationとは、1つか複数のソースドメインから知識を転移させて、ターゲットドメインのタスクの性能を向上させるプロセスである。つまり、Domain Adaptationを通して、Transfer Learningは実現される。
Transfer Learningのカテゴリ分け
大きく分けると以下の3つに分けられる。
- Transductive Transfer Learning ラベルの情報がソースドメインだけから得ている。
- Inductive Transfer Learning ラベルの情報がソース、ターゲットドメイン両方から得られる。
- Unsupervised Transfer Learning ラベルの情報がいずれも得られない場合。
Homogeneousかどうかだと、以下のように分けられる。以下のものがHomogeneous。
これ以外のもの、たとえばかはHeterogeneousとなる。
先行研究では、また具体的な手法についてのカテゴリ分けを提唱している。
- Instance Based 各サンプルについての重みづけを変更する系の手法。
- Feature Based もともとの特徴から新たな特徴を表現を作り出す。
- Asymmetric Feature Based ソースドメインの特徴をターゲットドメインの特徴に合致させるようにする。
- Symmetric Feature Based 新しい特徴空間を定義して、ソースドメイン、ターゲットドメイン両方の特徴をそこに合致させるようにする。
- Parameter Based モデルのパラメタをそのまま使うか、何かしらの変換を施す。
- Relational Based ソースドメインで存在するオブジェクト間の関係やパターンをターゲットドメインに適用する。
- 例えば、グラフの隣接の状況に基づくノードの関係を新しいグラフに転送するとか。
この論文では、Transfer Learningを
- Data Based Instance Based, Feature BasedのTransfer Learningを含む。
- Model Based 上記のParameter Basedである。
Relational Basedはこの論文ではあまり紹介しない。
Data Based Interpretation
Instance Based, Feature Basedについての手法紹介。
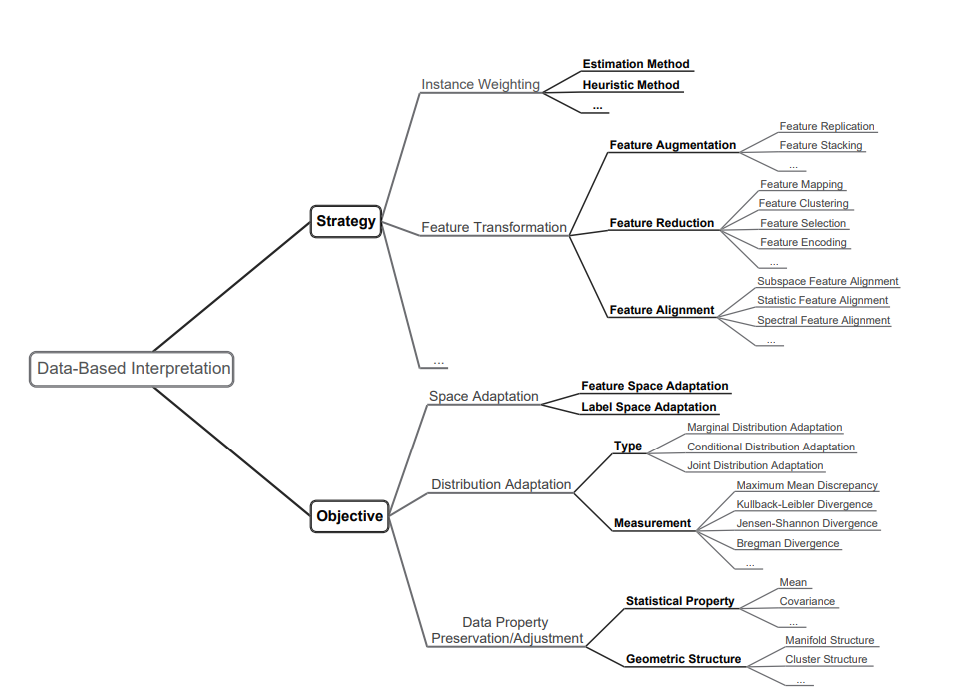
Instance Weighting Strategy
密度比推定
ソースドメインにおいて大量のラベルつきサンプルと、少数のラベルがないターゲットドメインのサンプルがあるとする。以下のように、周辺分布だけが違うCovariance Shiftを考える。
これを解決する一番簡単なアプローチは、以下のように密度比を推定して、変換すればいい。
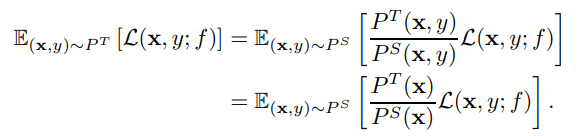
これについて、経験的に説くと以下のような形になる。は正則化項。
Kernel Mean Matching
同じく密度比推定でを推定するのだが、再生核ヒルベルト空間のうえにソース、ターゲット両方のドメインのデータをすべて写像したうえで、ソースとターゲット両方の分布の中心をできるだけ合致させるようにしている。
具体的には以下の最適化問題を解く。つまりの平均は1に近くなるようにする。は小さい値。
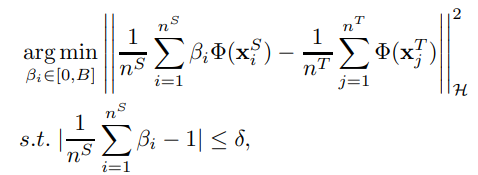
ただこれは中心だけ合わせているので、分布の回転や向きなどは考えていない。他にも、不均衡なサンプルに弱く外れ値にも弱いという欠点がある。
この合わせ方は、Maximum Mean Discrepancy(MMD)を最小化しているといえ、これの実現方法の1つにKernel Mean Matchingがある感じ?
KL Importance Estimation Procedure (KLIEP)
杉山先生のやつ。論文はこちらhttps://www.ism.ac.jp/editsec/aism/pdf/060_4_0699.pdf
ターゲットドメインのに対して、を合わせていく。この時、KLダイバージェンスを最小化させるのが目標である。ここで、密度比はであり、うまく推定していきたい(提案されていたのはSVMだった)
実質後者だけ最適化すればよく、これについて経験的に解く。ただし、重みについては先行研究と同じように、制約を設けている。
2段階のWeighting
2-Stage Weighting Framework for Multi-Source Domain Adaptation(2SW-MDA)
論文はこちら: https://papers.nips.cc/paper_files/paper/2011/hash/d709f38ef758b5066ef31b18039b8ce5-Abstract.html
合計個のSource Domainがあり、それぞれから知識を転用してTarget Domainに持っていきたい。Target DomainはUnlabeledであり、つまりTransductive Learningである。
2段階のWeightingをする。
- 各ソースドメインから、ターゲットドメインへ、変換する密度比をKMMなどで計算する。
- 各ドメインの推定した密度比が得られたので、これをまず使って学習をすることで、Source Domainについて、識別器が得られる。ターゲットデータの分布を各ドメインごと得られる。
- 平滑性の仮定に基づいて、各Domainの間の予測した分布は合致させたい。これをもとに、もう1つDomainに対しての重みを考える。
- だとして、ターゲットのサンプルについて、各による予測の分布はとする。このとき、以下の二次最小化問題を解く。
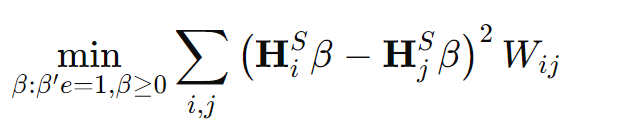
はサンプルとの間の類似度を表す行列で、これは点の距離とかでどうやらガウシアンカーネルで求めているらしい。
具体的にステップ2でどのように平滑性仮定を使うのか。
一例としてターゲットドメイン間の類似度を計算する。一例としてガウシアンカーネルで求めめる。
次に、ターゲットドメインのサンプルをノードとして、similarityを重みとしたグラフを定義し、
- が類似度行列で、
- は対角成分に各ノードがつながる辺の重みの総和
だとするとグラフラプラシアンはとなる。グラフラプラシアンについてはこのQiitaを参照。
ターゲットの重みを乗じた各ドメインのの計算をするが、最後に正則化項としてこの平滑性を意味するを加えることになる。
正則化項ではターゲットドメインについての計算であり、の訓練自体はステップ1で得た密度比によって各ソースドメインに所属するデータをターゲットドメインに変換して、訓練している。
TrAdaBoost
論文: https://dl.acm.org/doi/10.1145/1273496.1273521
AdaBoostでは毎イテレーション各サンプルの構成する損失のweightを、誤ったサンプルの重みを大きくするようにすることで効率的に学習できる。具体的には、以下のように重みを更新する。
ここでは分類器の重みであり、はサンプルの重みである。はそのバッチでの損失である。各サンプルについての重みはである。
ここに転移学習要素を入れると、ソースドメインとターゲットドメインの間で同じ基準で重みづけはできない。
- 毎イテレーションで、ターゲットドメインのラベルについての損失をとする。
- に応じて、以下のようにソースドメインとターゲットドメインの重みを更新する。
- いずれも一般的なAdaBoostの重み変更ではない。
- ソースドメインのデータの重み。サンプルの重みは、を使わずにサンプルが多いほど基数が高く、イテレーションの総数が大きいほど基数が低くなる。基数は1以下なので、指数が大きいほど重みが小さくなる。
- 指数部分は予測とラベルの差。ずれているほど指数が拡大される。
- ターゲットドメインのデータの重み。正解率が高いほど基数は下がっていく。
TrAdaBoostの拡張
論文: https://ieeexplore.ieee.org/abstract/document/5539857/
Multi-Source TrAdaBoost
複数のソースドメインがあるという問題設定。
- 弱学習器の集合をそれぞれ、の間で、TrAdaBoostで計算した今の重みを使って訓練する。
- 今の重みはステップ2で得る。
- 各ソースドメインとターゲットドメインの組み合わせで訓練した識別器について、一番ターゲットドメインでの誤分類率が低いものを選び、その分類器で全体のインスタンスの重みを更新する。
つまり、TrAdaBoostを複数のソースドメインで使うとき、重みは
各ソースドメインでの重みの更新は上の式のように自分自身に複数掛け合わせていくというものであるので、各ソースドメイン間で共通するのは、前の識別器を使った指数の肩のとして使うのは、一番ターゲットドメインで誤分類がすくないソースドメイン、ターゲットドメインの組み合わせということ。
Instance Weighting for Domain Adaptation
論文: https://aclanthology.org/P07-1034/
三種類のサンプルのクロスエントロピー損失を最小化することを提案している。
- Labeled Target Domain こちらは通常の学習と同じようにすればいい。
- Unlabeled Target Domain こちらは自己教師あり学習を用いて、Pseudo Labelを付与する。
- Labeled Source Domain KMMなどで密度比を推定する。そして、もう1つを定め、Domain適用の結果確信度が高いものを上からX割選ぶ。選ぶ、選ばないはで表現する。
